线性表
线性表(Linear List)是由一组数据元素按一定的顺序排列组成的集合。
线性表的基本操作
- 初始化:初始化线性表为空。
- 插入:在指定位置插入元素。
- 删除:删除指定位置的元素。
- 查找:查找某个元素的位置。
- 访问:通过索引访问指定位置的元素。
- 遍历:从头到尾依次访问线性表中的每个元素。
- 长度:获取线性表中的元素个数。
顺序表
顺序表是一种线性表的实现方式,其核心思想是将线性表中的元素存储在一块连续的内存空间中。
顺序表通常是使用数组来实现的,元素可以通过索引直接访问。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
| #include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
typedef struct {
int data[MAX_SIZE];
int length;
} SeqList;
void initSeqList(SeqList* list) {
list->length = 0;
}
int isEmpty(SeqList* list) {
return list->length == 0;
}
int isFull(SeqList* list) {
return list->length == MAX_SIZE;
}
int insert(SeqList* list, int index, int value) {
if (index < 0 || index > list->length || isFull(list)) {
return -1;
}
for (int i = list->length; i > index; --i) {
list->data[i] = list->data[i - 1];
}
list->data[index] = value;
list->length++;
return 0;
}
int delete(SeqList* list, int index) {
if (index < 0 || index >= list->length) {
return -1;
}
for (int i = index; i < list->length - 1; ++i) {
list->data[i] = list->data[i + 1];
}
list->length--;
return 0;
}
int find(SeqList* list, int value) {
for (int i = 0; i < list->length; ++i) {
if (list->data[i] == value) {
return i;
}
}
return -1;
}
int get(SeqList* list, int index) {
if (index < 0 || index >= list->length) {
return -1;
}
return list->data[index];
}
void printSeqList(SeqList* list) {
for (int i = 0; i < list->length; ++i) {
printf("%d ", list->data[i]);
}
printf("\n");
}
int getLength(SeqList* list) {
return list->length;
}
int main() {
SeqList list;
initSeqList(&list);
insert(&list, 0, 10);
insert(&list, 1, 20);
insert(&list, 2, 30);
insert(&list, 1, 15);
printSeqList(&list);
int index = find(&list, 20);
if (index != -1) {
printf("元素20在顺序表中的位置:%d\n", index);
} else {
printf("未找到元素20\n");
}
int value = get(&list, 2);
if (value != -1) {
printf("顺序表中索引2的元素是:%d\n", value);
}
delete(&list, 1);
printSeqList(&list);
return 0;
}
|
链表
单链表
每个节点包含两个部分:
- 数据域 (Data):存储节点的数据。
- 指针域 (Next):指向下一个节点的地址。
最后一个节点的 Next 指针通常为 NULL,表示链表的终点。
无链表头
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
| #include <stdio.h>
#include "stdlib.h"
typedef int E;
typedef struct Node{
E element;
struct Node *next;
}Node;
Node* createNode(E element){
Node *newNode = (Node*)malloc(sizeof(Node));
if(!newNode){
printf("内存分配失败!\n");
exit(EXIT_FAILURE);
}
newNode->element = element;
newNode->next = NULL;
return newNode;
}
Node* insertAtHead(Node *head,E element){
Node *newNode = createNode(element);
if(head==NULL){
head = newNode;
return head;
}
newNode->next = head;
return newNode;
}
Node* appendAtHead(Node *head,E element){
Node *newNode = createNode(element);
if(head==NULL){
head = newNode;
return head;
}
Node *temp = head;
while (temp->next!=NULL){
temp=temp->next;
}
temp->next = newNode;
return head;
}
Node* deleteNode(Node *head,E element){
Node *temp = head;
Node *prev = NULL;
if(temp!=NULL && temp->element==element){
head = head->next;
free(temp);
return head;
}
while (temp!=NULL && temp->element!=element){
prev = temp;
temp=temp->next;
}
if(temp==NULL){
printf("未找到值为 %d 的节点。\n", element);
return head;
}
prev->next=temp->next;
free(temp);
return head;
}
int queryNode(Node *head,E element){
Node *temp = head;
int count = 0;
while (temp->next!=NULL){
if(temp->element==element){
return count;
}
temp = temp->next;
count++;
}
return -1;
}
void printList(Node *head){
Node *temp = head;
while (temp!=NULL){
printf("%d->",temp->element);
temp = temp->next;
}
printf("NULL\n");
}
void freeList(Node *head){
Node *temp = head;
Node *next = NULL;
while (temp!=NULL){
next = temp->next;
free(temp);
temp = next;
}
head = NULL;
printf("free List");
}
int main() {
Node *head = NULL;
head = insertAtHead(head,7);
printf("%d\n",head->element);
head = appendAtHead(head,8);
printf("%d\n",head->next->element);
head = deleteNode(head,7);
printf("%d\n",head->element);
head = insertAtHead(head,7);
printf("%d\n",head->element);
head = deleteNode(head,8);
printf("%d\n",head->element);
int q = queryNode(head,9);
printf("%d\n",q);
printList(head);
freeList(head);
return 0;
}
|
有链表头
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
| #include <stdio.h>
#include "stdlib.h"
typedef int E;
typedef struct Node{
E element;
struct Node *next;
}Node;
Node* createNode(E element){
Node *newNode = (Node*)malloc(sizeof(Node));
if(!newNode){
printf("内存分配失败!\n");
exit(EXIT_FAILURE);
}
newNode->element = element;
newNode->next = NULL;
return newNode;
}
void insertAtHead(Node *head,E element){
Node *newNode = createNode(element);
if(head->next==NULL){
head->next=newNode;
return;
}
Node *temp = head->next;
head->next = newNode;
newNode->next = temp;
}
void appendAtHead(Node *head,E element){
Node *newNode = createNode(element);
Node *temp = head;
while (temp->next!=NULL){
temp=temp->next;
}
temp->next=newNode;
}
void deleteNode(Node *head,E element){
Node *temp = head;
while (temp->next!=NULL){
if(temp->next->element==element){
Node *del = temp->next;
temp->next = temp->next->next;
free(del);
break;
}
}
}
int queryNode(Node* head,E element){
Node *temp = head;
int count =1;
while (temp->next!=NULL){
if(temp->next->element==element){
return count;
}
temp=temp->next;
count++;
}
return -1;
}
void printList(Node* head){
Node *temp = head;
while (temp->next!=NULL){
printf("%d->",temp->next->element);
temp = temp->next;
}
printf("NULL\n");
}
void freeList(Node *head){
Node *temp = head;
Node *next = NULL;
while (temp!=NULL){
next = temp->next;
free(temp);
temp = next;
}
head = NULL;
printf("free List");
}
int main(){
Node *head = (Node*)malloc(sizeof(Node));
head->element=0;
head->next=NULL;
insertAtHead(head,7);
printf("%d\n",head->next->element);
appendAtHead(head,8);
printf("%d\n",head->next->next->element);
deleteNode(head,7);
printf("%d\n",head->next->element);
appendAtHead(head,7);
printf("%d\n", queryNode(head,7));
printList(head);
freeList(head);
return 0;
}
|
双向链表
双向链表的每个节点包含两个指针:
- 一个指向前驱节点(prev)。
- 一个指向后继节点(next)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
| #include <stdio.h>
#include "stdlib.h"
typedef int E;
typedef struct Node{
E element;
struct Node *next;
struct Node *prev;
}Node;
void initList(Node* head){
head->element=0;
head->next=NULL;
head->prev=NULL;
}
Node* createNode(E element){
Node *newNode = (Node*)malloc(sizeof(Node));
if(!newNode){
printf("内存分配失败!\n");
exit(EXIT_FAILURE);
}
newNode->element = element;
newNode->next = NULL;
newNode->prev = NULL;
return newNode;
}
void insertAtHead(Node *head,E element){
Node *newNode = createNode(element);
if(head->next==NULL){
head->next=newNode;
newNode->prev=head;
return;
}
Node *temp = head->next;
head->next = newNode;
newNode->prev = head;
newNode->next = temp;
temp->prev = newNode;
}
void appendAtHead(Node *head,E element){
Node *newNode = createNode(element);
Node *temp = head;
while (temp->next!=NULL){
temp=temp->next;
}
temp->next=newNode;
newNode->prev = temp;
}
void deleteNode(Node *head,E element){
Node *temp = head;
while (temp->next!=NULL){
if(temp->next->element==element){
Node *del = temp->next;
temp->next = temp->next->next;
temp->next->prev = temp;
free(del);
return;
}
temp = temp->next;
}
printf("can't find %d\n", element);
}
int queryNode(Node* head,E element){
Node *temp = head;
int count =1;
while (temp->next!=NULL){
if(temp->next->element==element){
return count;
}
temp=temp->next;
count++;
}
return -1;
}
void printList(Node* head){
Node *temp = head;
while (temp->next!=NULL){
printf("%d->",temp->next->element);
temp = temp->next;
}
printf("NULL\n");
}
void freeList(Node *head){
Node *temp = head;
Node *next = NULL;
while (temp!=NULL){
next = temp->next;
free(temp);
temp = next;
}
head = NULL;
printf("free List");
}
int main(){
Node *head = (Node*)malloc(sizeof(Node));
initList(head);
insertAtHead(head,7);
printf("%d\n",head->next->element);
appendAtHead(head,8);
printf("%d\n",head->next->next->element);
deleteNode(head,7);
printf("%d\n",head->next->element);
appendAtHead(head,7);
printf("%d\n", queryNode(head,7));
printList(head);
freeList(head);
}
|
循环链表
循环链表的最后一个节点指向头节点,从而形成一个环状结构。
在循环链表中,任何一个节点的下一个节点都不会是NULL。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
| #include <stdio.h>
#include "stdlib.h"
typedef int E;
typedef struct Node{
E element;
struct Node *next;
}Node;
void initList(Node* head){
head->element=0;
head->next=head;
}
Node *createNode(E element){
Node *newNode = (Node*)malloc(sizeof(Node));
if(!newNode){
printf("内存分配失败!\n");
exit(EXIT_FAILURE);
}
newNode->element = element;
newNode->next=NULL;
return newNode;
}
void insertAtHead(Node *head,E element){
Node *newNode = createNode(element);
head->next = newNode;
newNode->next = head;
}
void appendAtHead(Node *head,E element){
Node *newNode = createNode(element);
Node *temp = head;
while (temp->next!=head){
temp=temp->next;
}
temp->next=newNode;
newNode->next = head;
}
void deleteNode(Node *head,E element){
Node *temp = head;
while (temp->next!=head){
if(temp->next->element==element){
Node *del = temp->next;
temp->next = temp->next->next;
free(del);
return;
}
temp = temp->next;
}
printf("can't find %d\n", element);
}
int queryNode(Node* head,E element){
Node *temp = head;
int count =1;
while (temp->next!=head){
if(temp->next->element==element){
return count;
}
temp=temp->next;
count++;
}
return -1;
}
void printList(Node* head){
Node *temp = head;
while (temp->next!=head){
printf("%d->",temp->next->element);
temp = temp->next;
}
printf("NULL\n");
}
void freeList(Node *head){
Node *temp = head->next;
Node *next = NULL;
while (temp!=head){
next = temp->next;
free(temp);
temp = next;
}
free(head);
head = NULL;
printf("free List");
}
int main(){
Node *head = (Node*)malloc(sizeof(Node));
initList(head);
insertAtHead(head,7);
printf("%d\n",head->next->element);
appendAtHead(head,8);
printf("%d\n",head->next->next->element);
deleteNode(head,7);
printf("%d\n",head->next->element);
appendAtHead(head,7);
printf("%d\n", queryNode(head,7));
printList(head);
freeList(head);
}
|
栈与队列
栈
栈遵循后进先出的原则
顺序结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #include "stdio.h"
#include "stdlib.h"
#define MAX_SIZE 100
typedef int E;
typedef struct Stack {
int data[MAX_SIZE];
int top;
} Stack;
void initStack(Stack *stack) {
stack->top = -1;
}
int isNull(Stack *stack) {
if (stack->top == -1) {
return 1;
}
return 0;
}
void push(Stack *stack, E element) {
stack->top = stack->top + 1;
if (stack->top >= MAX_SIZE) {
printf("out of MAX_SIZE!\n");
stack->top--;
return;
}
stack->data[stack->top] = element;
}
int pop(Stack *stack, E *e) {
if (isNull(stack)) {
printf("stack is NULL!\n");
return 0;
}
*e = stack->data[stack->top];
stack->top = stack->top - 1;
return 1;
}
int peek(Stack *stack, E *e) {
if (isNull(stack)) {
printf("stack is NULL!\n");
return 0;
}
*e = stack->data[stack->top];
return 1;
}
int main() {
Stack *stack = (Stack *) malloc(sizeof(Stack));
initStack(stack);
push(stack, 7);
printf("%d\n", stack->data[stack->top]);
E *e = (E *) malloc(sizeof(E));
pop(stack, e);
printf("%d\n", *e);
push(stack, 8);
peek(stack, e);
printf("%d\n", *e);
free(stack);
free(e);
return 0;
}
|
链式结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| #include "stdio.h"
#include "stdlib.h"
typedef int E;
typedef struct Stack {
E data;
struct Stack* next;
} Stack;
void initStack(Stack *head) {
head->data = 0;
head->next = NULL;
}
Stack* createStack(E element) {
Stack *stack = (Stack*) malloc(sizeof(Stack));
stack->next = NULL;
stack->data = element;
return stack;
}
int isNULL(Stack* head) {
if (head->next == NULL) {
return 1;
}
return 0;
}
void pushStack(Stack* head, E element) {
Stack *temp = head->next;
Stack *newNode = createStack(element);
head->next = newNode;
newNode->next = temp;
}
E popStack(Stack* head) {
if (isNULL(head)) {
printf("Stack is NULL\n");
return 0;
}
Stack *temp = head->next;
head->next = head->next->next;
E e = temp->data;
free(temp);
return e;
}
void printStack(Stack* head) {
Stack *temp = head->next;
while (temp != NULL) {
printf("%d->", temp->data);
temp = temp->next;
}
printf("NULL\n");
}
void freeStack(Stack* head) {
Stack *temp = head->next;
while (temp != NULL) {
free(head);
temp = temp->next;
head = temp;
}
printf("Stack is NULL\n");
}
int main() {
Stack *head = (Stack*) malloc(sizeof(Stack));
initStack(head);
pushStack(head, 7);
printf("%d\n", head->next->data);
pushStack(head, 8);
printf("%d\n", head->next->data);
E e = popStack(head);
printf("%d\n", e);
printStack(head);
freeStack(head);
return 0;
}
|
队列
队列遵循先进先出的原则
顺序结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
| #include "stdio.h"
#include "stdlib.h"
#define MAX_SIZE 5
typedef int E;
typedef struct Queue {
int data[MAX_SIZE];
int front;
int rear;
int size;
} Queue;
void initQueue(Queue *queue) {
queue->front = 0;
queue->rear = 0;
queue->size = 0;
}
int isEmpty(Queue *queue) {
if (queue->size == 0) {
printf("Queue is NULL!\n");
return 1;
}
return 0;
}
int isFull(Queue *queue) {
if (queue->size == MAX_SIZE) {
printf("Queue is FULL!\n");
return 1;
}
return 0;
}
void enQueue(Queue *queue, E element) {
if (isFull(queue)) {
printf("Queue is FULL!\n");
return;
}
queue->data[queue->rear] = element;
queue->rear = (queue->rear + 1) % MAX_SIZE;
queue->size++;
}
E deQueue(Queue *queue) {
if (isEmpty(queue)) {
return -1;
}
E e = queue->data[queue->front];
queue->front = (queue->front + 1) % MAX_SIZE;
queue->size--;
return e;
}
void printQueue(Queue *queue) {
if (isEmpty(queue)) {
return;
}
printf("Queue elements: ");
int size = queue->size;
int temp = queue->front;
while (size != 0) {
printf("%d->", queue->data[temp]);
temp = (temp + 1) % MAX_SIZE;
size--;
}
printf("NULL\n");
}
int main() {
Queue *queue = (Queue *)malloc(sizeof(Queue));
initQueue(queue);
enQueue(queue, 1);
printf("%d\n", queue->data[0]);
enQueue(queue, 2);
printf("%d\n", queue->data[1]);
enQueue(queue, 3);
enQueue(queue, 4);
enQueue(queue, 5);
printf("%d\n", queue->size);
printQueue(queue);
E e;
e = deQueue(queue);
printf("%d\n", e);
e = deQueue(queue);
printf("%d\n", e);
e = deQueue(queue);
printf("%d\n", e);
free(queue);
return 0;
}
|
链式结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
| #include "stdio.h"
#include "stdlib.h"
typedef int E;
typedef struct Node {
E element;
struct Node* next;
} Node;
typedef struct Queue {
Node *front;
Node *rear;
} Queue;
void initQueue(Queue* queue) {
queue->rear = NULL;
queue->front = NULL;
}
int isEmpty(Queue* queue) {
return (queue->front == NULL);
}
Node *createNode(E element) {
Node *newNode = (Node*) malloc(sizeof(Node));
newNode->next = NULL;
newNode->element = element;
return newNode;
}
void enQueue(Queue* queue, E element) {
Node *newNode = createNode(element);
if (isEmpty(queue)) {
queue->front = newNode;
queue->rear = newNode;
return;
}
queue->rear->next = newNode;
queue->rear = newNode;
}
E deQueue(Queue* queue) {
if (isEmpty(queue)) {
printf("Queue is NULL\n");
return -1;
}
E e = queue->front->element;
Node *deNode = queue->front;
queue->front = deNode->next;
free(deNode);
return e;
}
void freeQueue(Queue* queue) {
Node *temp = queue->front;
while (temp != NULL) {
queue->front = queue->front->next;
free(temp);
temp = queue->front;
}
free(queue);
printf("free Queue!\n");
}
int main() {
Queue *queue = (Queue *)malloc(sizeof(Queue));
initQueue(queue);
enQueue(queue, 7);
enQueue(queue, 8);
E e = deQueue(queue);
printf("Dequeued: %d\n", e);
e = deQueue(queue);
printf("Dequeued: %d\n", e);
e = deQueue(queue);
printf("Dequeued: %d\n", e);
freeQueue(queue);
return 0;
}
|
树
树的定义
树(Tree)是有n个节点的有限集,它或为空树(n=0),或为非空树(n>0)。
有且只有一个根节点。
除根节点以外的节点可以分为m个互不相交的有限集,其中每一个集合本身又是一棵树,称为根的子树。
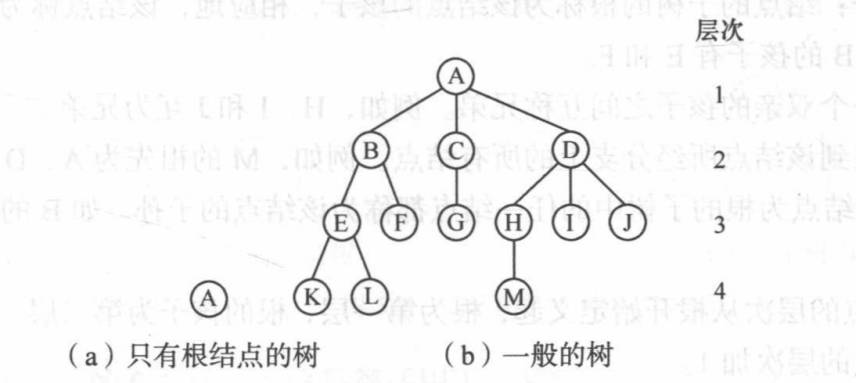
树的基本术语
结点
树中的一个独立单元。包含一个数据元素及若干指向其子树的分支。
结点的度
结点拥有的子树数称为结点的度。
树的度
树的度是树内各结点度的最大值。
叶子
度为0的结点称为叶子或终端结点。
非终端结点
度不为0的结点称为非终端结点或分支结点。
双亲和孩子
结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。
兄弟
同一个双亲的孩子之间互称兄弟。
祖先
从根到该结点所经分支上的所有结点。
子孙
以某结点为根的子树中的任一结点都称为该结点的子孙。
层次
结点的层次从根开始定义起,根为第一层,根的孩子为第二层。
树中任一结点的层次等于其双亲结点的层次加1。
堂兄弟
双亲在同一层的结点互为堂兄弟。
树的深度
树中结点的最大层次称为树的深度或高度。
有序数和无序树
如果将树中结点的各子树看成从左至右是有次序的(即不能互换), 则称该树为有序树,否则称为无序树。
在有序树中最左边的子树的根称为第一个孩子,最右边的称为最后一个孩子。
森林
是m (m≥0) 棵互不相交的树的集合。对树中每个结点而言,其子树的集合即 为森林。
二叉树的定义
二叉树(Binary Tree)是n个结点所构成的集合,它或为空树,或为非空树。
有且仅有一个称之为根的节点。
除根结点以外的其余结点分为两个互不相交的子集T1和T2,分别称为T的左子树和右子树,且T1和T2本身又都是二叉树。
二叉树与树的区别:
二叉树每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点);
二叉树的子树有左右之分,其次序不能任意颠倒。
二叉树的递归定义表明二叉树或为空,或是由一个根结点加上两棵分别称为左子树和右子树 的、互不相交的二叉树组成。由于这两棵子树也是二叉树,则由二叉树的定义,它们也可以是空树。

二叉树的性质


遍历二叉树
先序遍历、中序遍历、后续遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include "iostream"
using namespace std;
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x),left(nullptr),right(nullptr){}
};
void preorderRecursive(TreeNode(* root)){
if(!root) return;
cout << root->val << " ";
preorderRecursive(root->left);
preorderRecursive(root->right);
}
void inorderRecursive(TreeNode(* root)){
if(!root) return;
inorderRecursive(root->left);
cout << root->val << " ";
inorderRecursive(root->right);
}
void postorderRecursive(TreeNode(* root)){
if(!root) return;
postorderRecursive(root->left);
postorderRecursive(root->right);
cout << root->val << " ";
}
TreeNode* createTree(){
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
return root;
}
int main(){
TreeNode* root = createTree();
cout << "preorderRecursive: ";
preorderRecursive(root);
cout<<endl;
cout << "inorderRecursive: ";
inorderRecursive(root);
cout<<endl;
cout << "postorderRecursive: ";
postorderRecursive(root);
cout<<endl;
return 0;
}
|
线索二叉树
前序线索二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include "iostream"
using namespace std;
struct ThreadedNode {
int val;
ThreadedNode* left;
ThreadedNode* right;
int leftTag;
int rightTag;
ThreadedNode(int x) : val(x),left(nullptr),right(nullptr){}
};
ThreadedNode* pre = nullptr;
void preThread(ThreadedNode* node) {
if (!node) return;
if (!node->left) {
node->left = pre;
node->leftTag = 1;
}
if (pre && !pre->right) {
pre->right = node;
pre->rightTag = 1;
}
pre = node;
if (node->leftTag == 0) preThread(node->left);
if (node->rightTag == 0) preThread(node->right);
}
void threadedPreorder(ThreadedNode* root) {
ThreadedNode* curr = root;
while (curr) {
cout << "threadedPreorder" <<curr->val << " ";
if (curr->leftTag == 0) {
curr = curr->left;
} else {
curr = curr->right;
}
}
}
ThreadedNode* createTree(){
ThreadedNode* root = new ThreadedNode(1);
root->left = new ThreadedNode(2);
root->right = new ThreadedNode(3);
root->left->left = new ThreadedNode(4);
root->left->right = new ThreadedNode(5);
root->right->left = new ThreadedNode(6);
return root;
}
int main(){
ThreadedNode* threadedNode = createTree();
preThread(threadedNode);
threadedPreorder(threadedNode);
return 0;
}
|
中序线索二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| #include "iostream"
using namespace std;
struct ThreadedNode {
int val;
ThreadedNode* left;
ThreadedNode* right;
int leftTag;
int rightTag;
ThreadedNode(int x) : val(x),left(nullptr),right(nullptr){}
};
ThreadedNode* pre = nullptr;
void inThread(ThreadedNode* node) {
if (!node) return;
inThread(node->left);
if (!node->left) {
node->left = pre;
node->leftTag = 1;
}
if (pre && !pre->right) {
pre->right = node;
pre->rightTag = 1;
}
pre = node;
inThread(node->right);
}
void threadedInorder(ThreadedNode* root) {
ThreadedNode* curr = root;
while (curr) {
while (curr->leftTag == 0) {
curr = curr->left;
}
cout << curr->val << " ";
while (curr->rightTag == 1) {
curr = curr->right;
cout << curr->val << " ";
}
curr = curr->right;
}
}
ThreadedNode* createTree(){
ThreadedNode* root = new ThreadedNode(1);
root->left = new ThreadedNode(2);
root->right = new ThreadedNode(3);
root->left->left = new ThreadedNode(4);
root->left->right = new ThreadedNode(5);
root->right->left = new ThreadedNode(6);
return root;
}
int main(){
ThreadedNode* threadedNode = createTree();
inThread(threadedNode);
threadedInorder(threadedNode);
return 0;
}
4 2 5 1 6 3
|
树的存储结构
有多种形式的存储结构来表示树。
双亲表示法
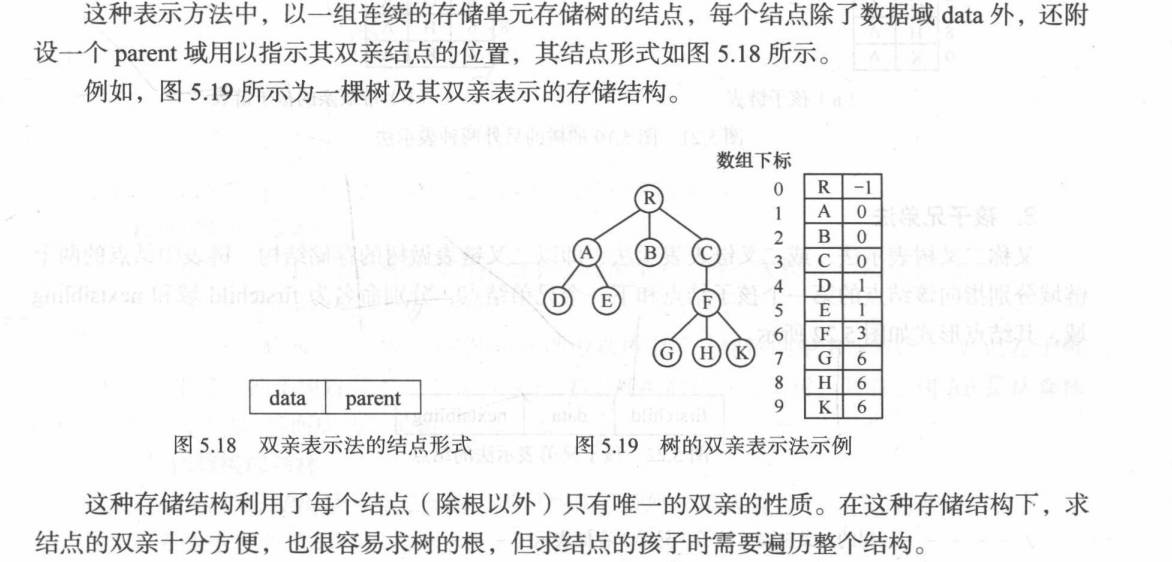
孩子表示法

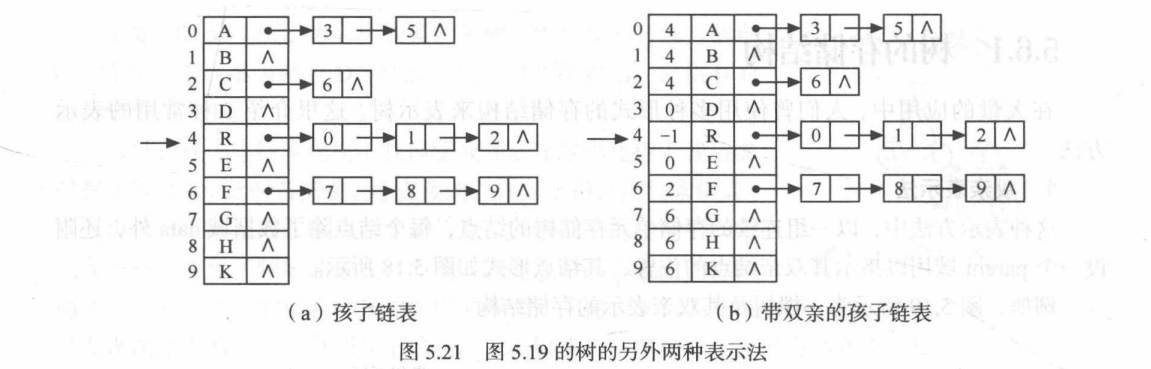
孩子兄弟法

哈夫曼树
哈夫曼树(Huffman Tree),又称最优二叉树,是一种带权路径长度(Weighted Path Length, WPL)最小的二叉树。
核心目标:用最小的编码长度表示频率高的字符,广泛应用于数据压缩(如哈夫曼编码)。







