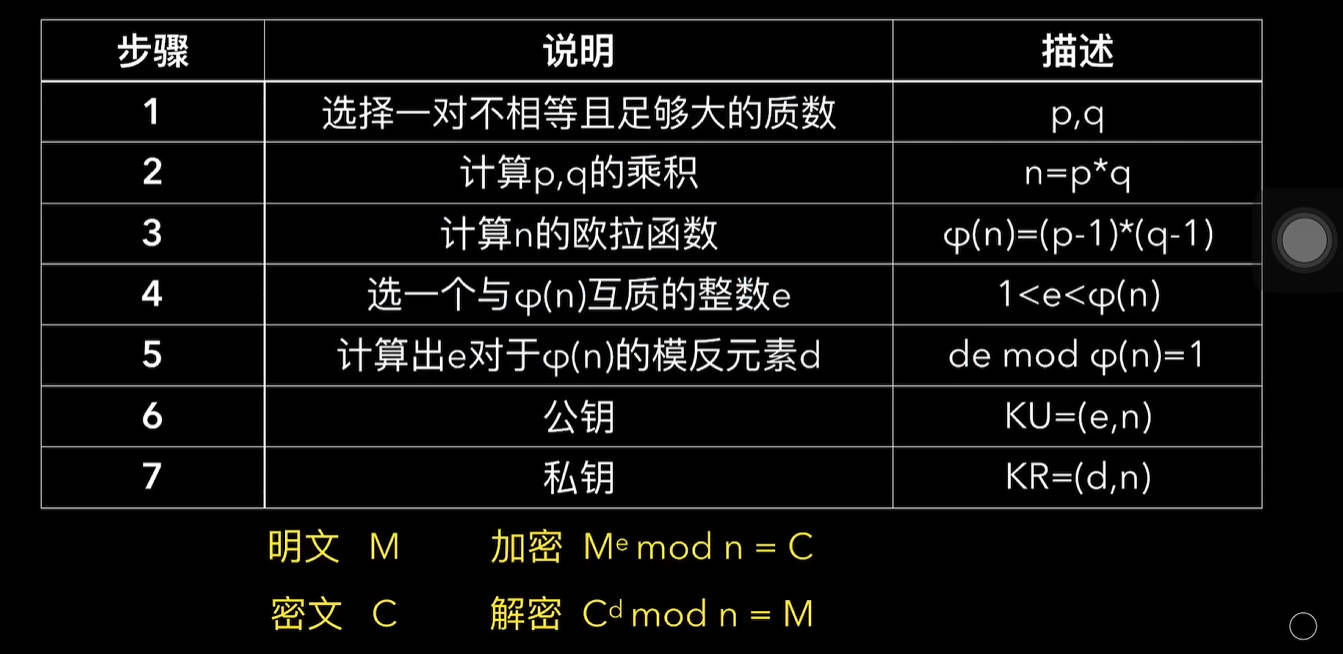
RSA介绍
RSA是一种非对称加密算法,广泛应用于数据加密和数字签名。其安全性基于大整数分解的数学难题:将两个大质数相乘容易,但分解乘积还原质数极其困难。
非对称加密
- 公钥:公开用于加密。
- 私钥:保密用于解密。
数学基础
- 欧拉定理:若a与n互质,则a**ϕ(n)≡1modn,其中ϕ(n)是欧拉函数。
- 模反元素:若e与ϕ(n)互质,则存在d使得e⋅d≡1modϕ(n)。
欧拉函数
欧拉函数,记作 φ(n),是数论中的一个核心概念,用于计算小于n且与n互质的正整数的个数。
模反元素
模反元素,简称模逆元,它描述了一个数在模运算下“可逆”的性质。
- 若整数 a 和 n 互质(即 gcd(a,n)=1),则存在整数 b,使得:a⋅b≡1modn
- 此时,b 称为 a 在模 n 下的模反元素(或称逆元),记作 a−1modn。
通俗理解:
在模 n 的算术体系中,a 的逆元 b 相当于“倒数”,使得 a⋅b 的余数为1。
示例:在模7下,3的逆元是5,因为 3×5=15≡1mod7。
加密流程