白乐天

道阻且长，行则将至。

详解TEA

发表于 分类于
本文字数： 1.8k 阅读时长 ≈ 2 分钟

TEA简介

TEA（Tiny Encryption Algorithm）是一种对称密钥分组密码算法。

分组长度：64位（8字节）（明文分为两个32位块，密文分为两个32位块）。

密钥长度：128位（16字节）（分为四个32位子密钥）。

加密流程

初始化

  • 将64位明文分为两部分：L0（左32位）和 R0（右32位）。

  • 初始化轮常量：δ=0x9E3779B9（黄金比例相关常数，用于增强非线性）。

  • 初始化累加变量：sum=0。

轮迭代（64轮）

对于每一轮i（从0到63）

1.更新累加变量

1
sum=sum+δ

2.更新左半部分

1
L(i+1)=Ri

3.更新右半部分

1
Ri+1=Li+F(Ri,sum,K)

轮函数F

1
F(Ri,sum,K)=((Ri<<4)+Kleft)⊕(Ri+sum)⊕((Ri>>5)+Kright)

Kleft和Kright

1
2
偶数轮（i为偶数）：Kleft=K[0], Kright=K[1]
奇数轮（i为奇数）：Kleft=K[2], Kright=K[3]

合并

经过64轮后，密文为左右部分合并

1
Ciphertext=(L64∣∣R64)

XTEA简介

XTEA（Extended TEA）是TEA（Tiny Encryption Algorithm）的改进版本。

  1. 密钥调度：引入更复杂的子密钥生成逻辑，避免密钥相关攻击。
  2. 轮函数：调整位移和混合操作的顺序，增强非线性性和扩散性。
  3. 轮常量计算：优化轮常量的使用方式，减少数学规律性。

算法参数

  • 分组长度：64位（分为两个32位块 L 和 R）。
  • 密钥长度：128位（16字节）（分为四个32位子密钥 K[0],K[1],K[2],K[3]）。
  • 加密轮数：通常为 64轮（Feistel结构）。
  • 安全性：抗相关密钥攻击和已知明文攻击，理论安全性优于TEA。

加密流程

XTEA采用 Feistel结构，每轮操作更新左右两部分数据。

初始化

  • 明文分为两个32位块：L0（左）和 R0（右）。
  • 轮常量：δ=0x9E3779B9（黄金比例相关常数）。
  • 累加变量：sum=0。

64轮迭代

对于每轮 i（从0到63）：

更新左半部分

1
Li+1=Li+(((Ri≪4)⊕(Ri≫5))+Ri)⊕(sum+K[(sum≫11)&3])

更新累加变量

1
sum=sum+δ

更新右半部分

1
Ri+1=Ri+(((Li+1≪4)⊕(Li+1≫5))+Li+1)⊕(sum+K[sum&3])

合并

经过64轮后，密文为左右部分合并：

1
Ciphertext=(L64∣∣R64)

XXTEA简介

XXTEA（Corrected Block TEA）是TEA算法的最终改进版本,旨在解决TEA和XTEA在处理 可变长度数据块 时的局限性。它支持任意长度的数据块（最小64位），并在混合操作中引入更复杂的非线性逻辑，显著提升了安全性。

核心改进

  1. 支持可变长度数据块：可加密任意长度（≥64位）的数据，无需固定分组。
  2. 增强的混合操作：通过多次位移和异或操作，强化非线性扩散。
  3. 优化的密钥调度：密钥参与更分散，避免局部性弱点。

算法参数

  • 数据块长度：任意长度（最小64位，即8字节）。
  • 密钥长度：128位（16字节）（分为四个32位子密钥 K[0],K[1],K[2],K[3]）。
  • 推荐轮数：通常为 52轮（根据数据块长度动态调整）。
  • 安全性：抗已知明文攻击和选择密文攻击，安全性优于XTEA。

加密流程

XXTEA采用 整块混合迭代 而非Feistel结构，所有数据字参与每轮计算。

初始化

  • 将明文分为 n 个32位字（v0,v1,…,v**n−1），n≥2。
  • 定义轮常量：δ=0x9E3779B9
  • 累加变量 sum=0。

预处理轮次

计算初始轮次：

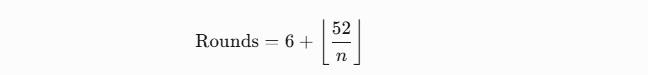
例如：n=4（128位数据块）→ Rounds = 6 + 13 = 19轮。

轮迭代（每轮更新所有字）

对于每轮 i（从0到Rounds-1）：

更新累加变量

1
sum=sum+δ

计算密钥混合索引

1
e=(sum≫2)&3

逐字更新数据块

对于每个字 vj（j 从0到 n−1）：

1
vj=vj+(((vj−1≪4)⊕(vj+1≫5))+vj+1)⊕(sum+K[(j&3)⊕e])

边界处理：

  • v−1=vn−1（当 j=0 时）。
  • vn=v0（当 j=n−1 时）。