基础?
幂函数

幂函数转根号

指数函数

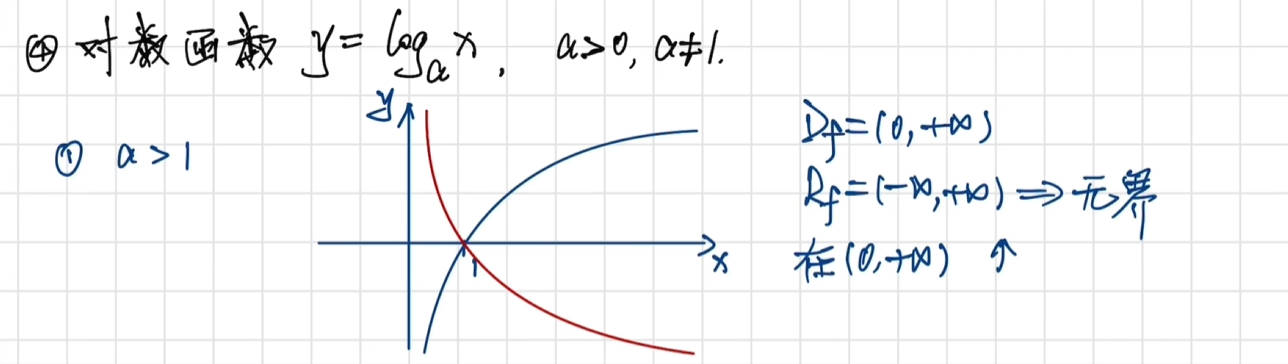
对数函数





图像
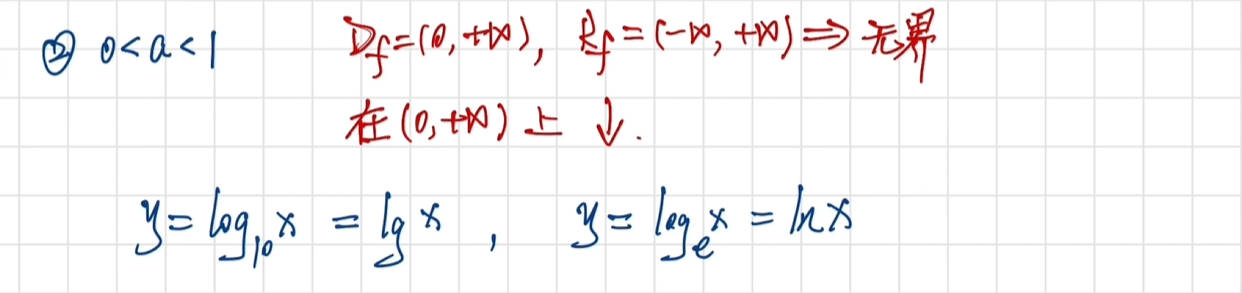
三角函数

三角函数特殊角值

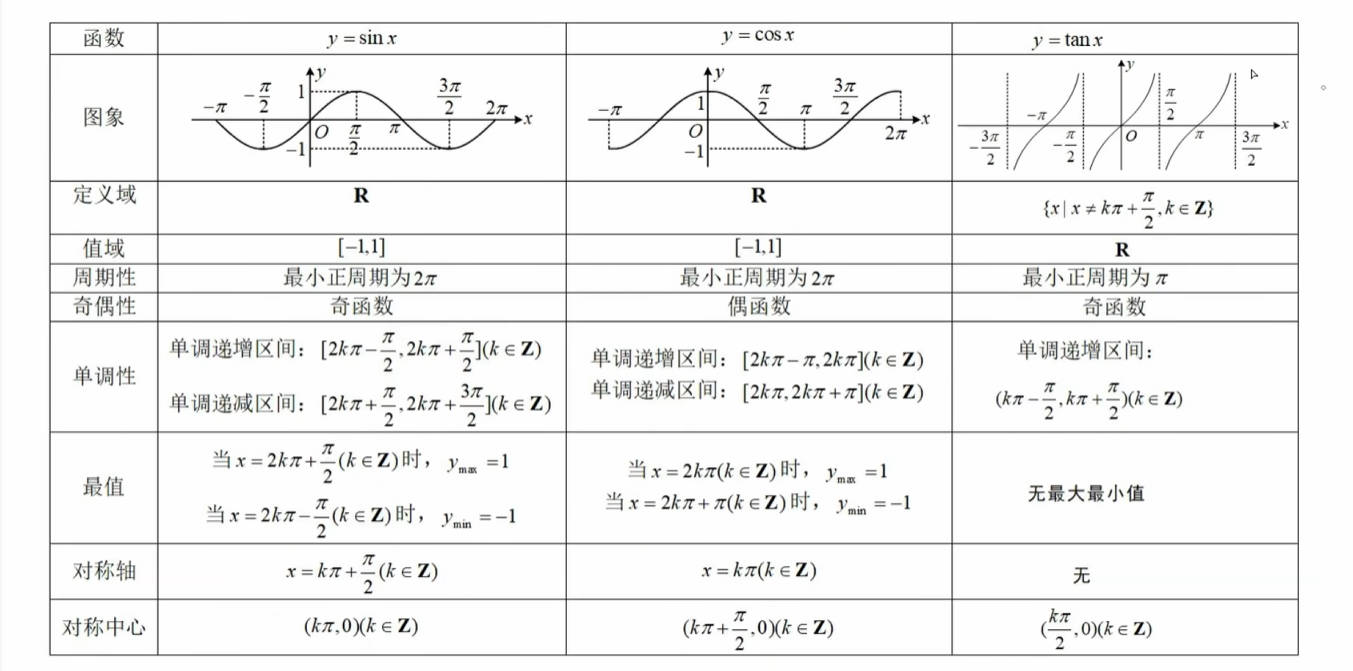
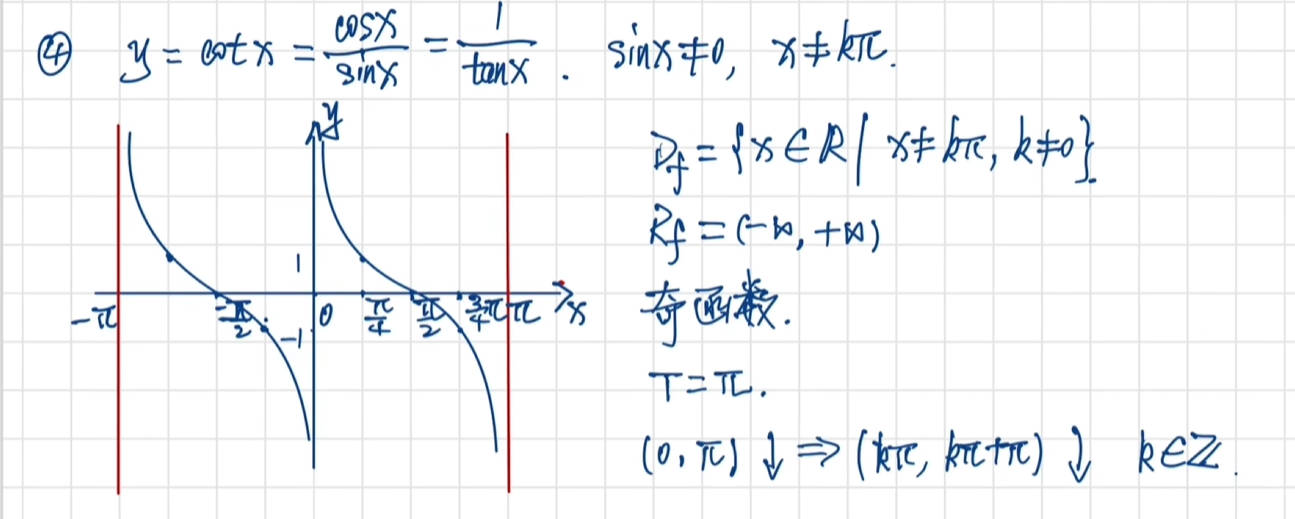
三角函数图像及性质
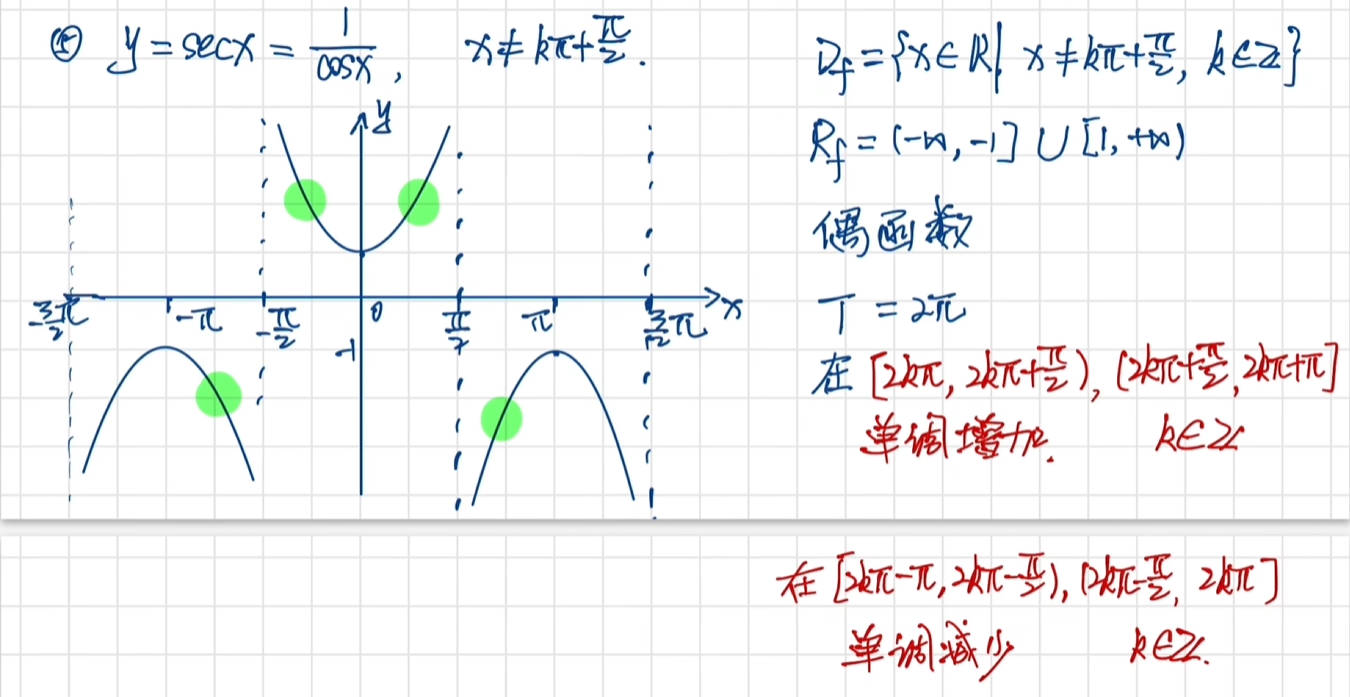
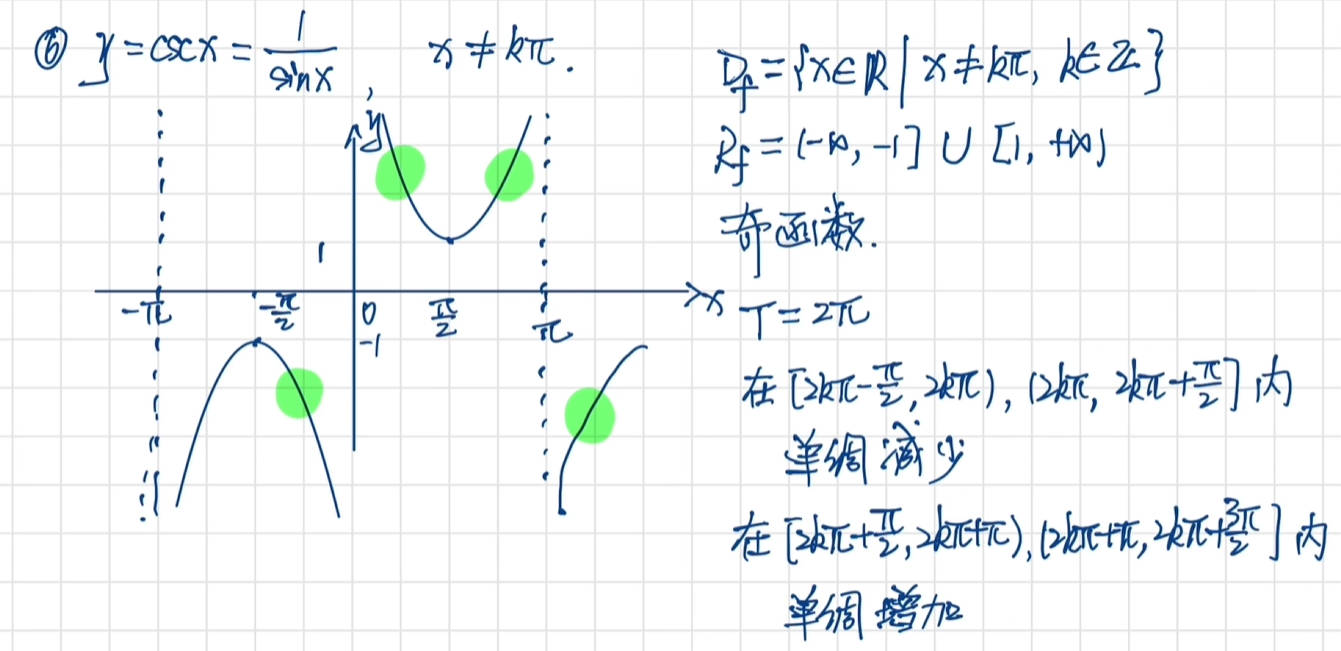
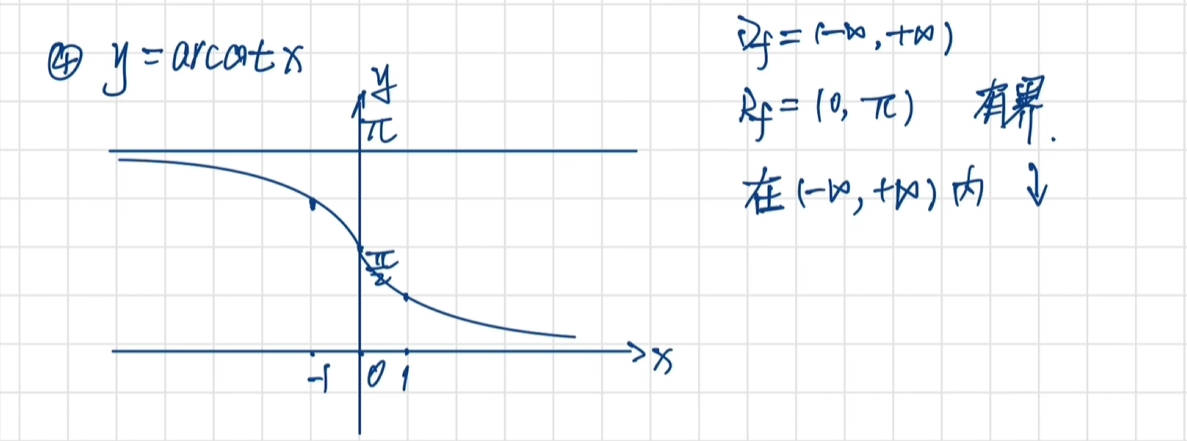
反三角函数图像及性质
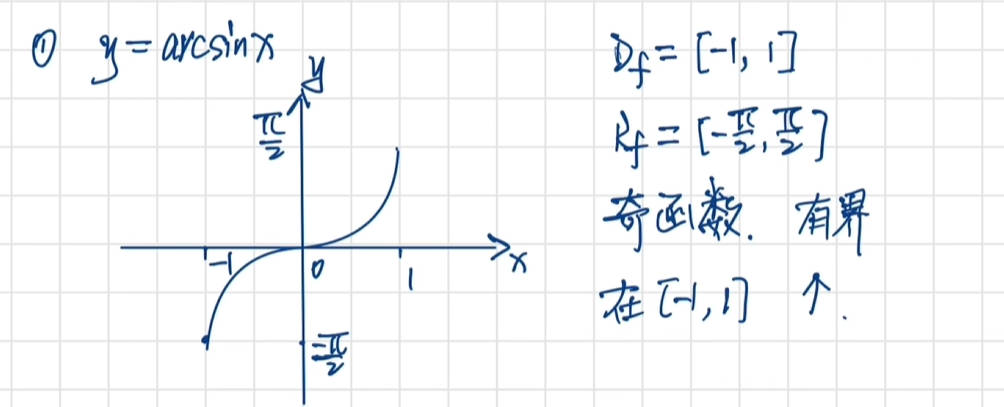

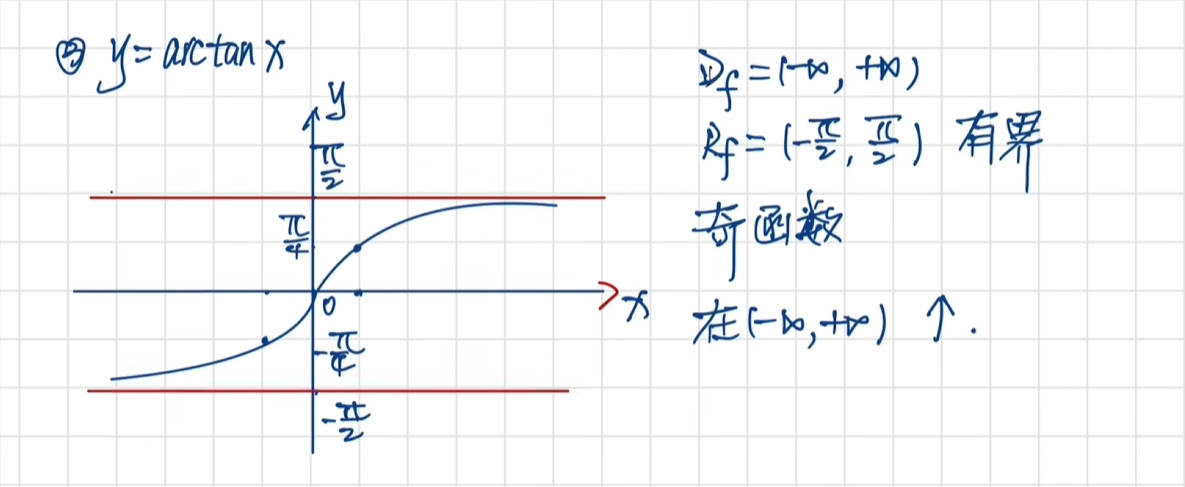
预备知识

奇变偶不变,符号看象限
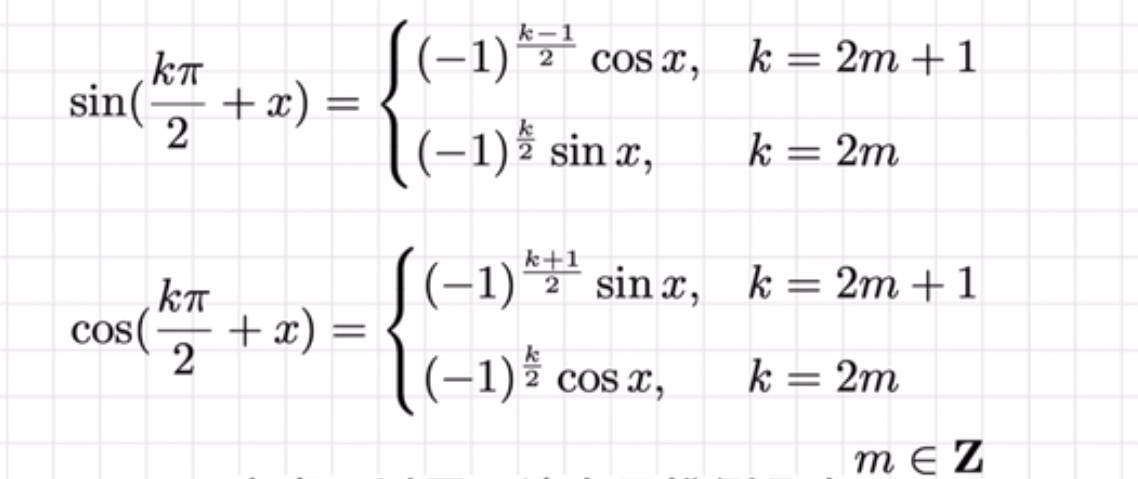





三角公式

判断函数奇偶性

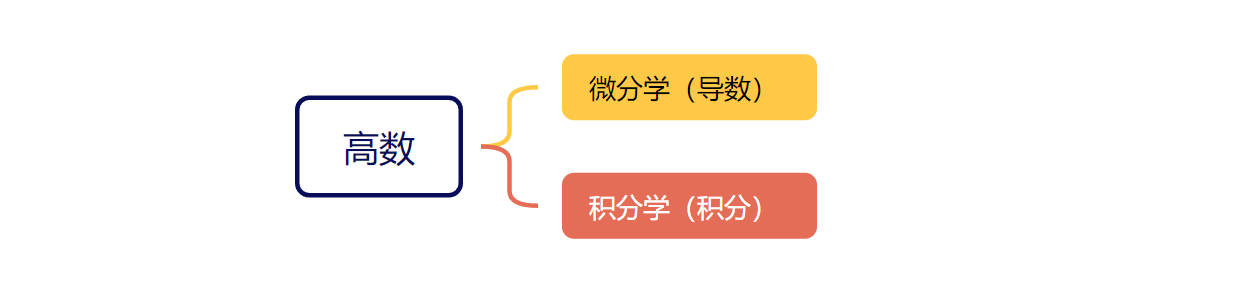
高数
微积分的主要研究内容
事物运动中的数量变化规律
两种变化
均匀变化
非均匀变化
两个侧面
微观(局部)
宏观(整体)
微积分的主要研究对象
函数y=f(x) (a<=x<=b)的变化规律
微观(变化率)
宏观(变化量)
思想方法
利用已知求未知
通过均匀变化求非均匀变化
局部均匀化求近似,利用极限得精确
微分和积分分别是处理均匀量的商和积在处理非均匀量中的发展
函数与极限
函数
给定两个非空集合 X 和 Y,函数(或映射) f 是一种规则,使得对于集合 XXX 中的任一元素 xxx ,都存在唯一一个元素 y∈Y与之对应,这个对应关系记作y=f(x).
- 定义域:(Domain):所有可以作为函数 f 输入的 x 的集合,即 X。
- 值域(Range 或 Image):函数f实际取值的集合
- 对应关系:对于每个 x∈X,存在唯一的 y∈Y使得 f(x)=y。
通过定义域和对应关系可以确定一个函数。
举例常见函数
绝对值函数
符号函数
取整函数
函数的几种特性
有界性
单调性
奇偶性
周期性
反函数与复合函数

原函数与它的反函数关于y=x对称

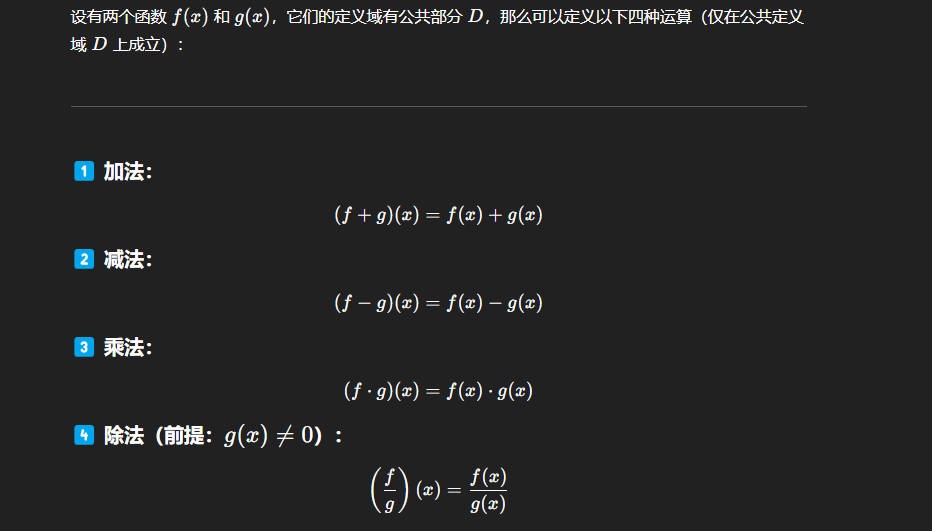
函数的运算
初等函数
将幂函数,指数函数,对数函数,三角函数,反三角函数统称为初等函数。
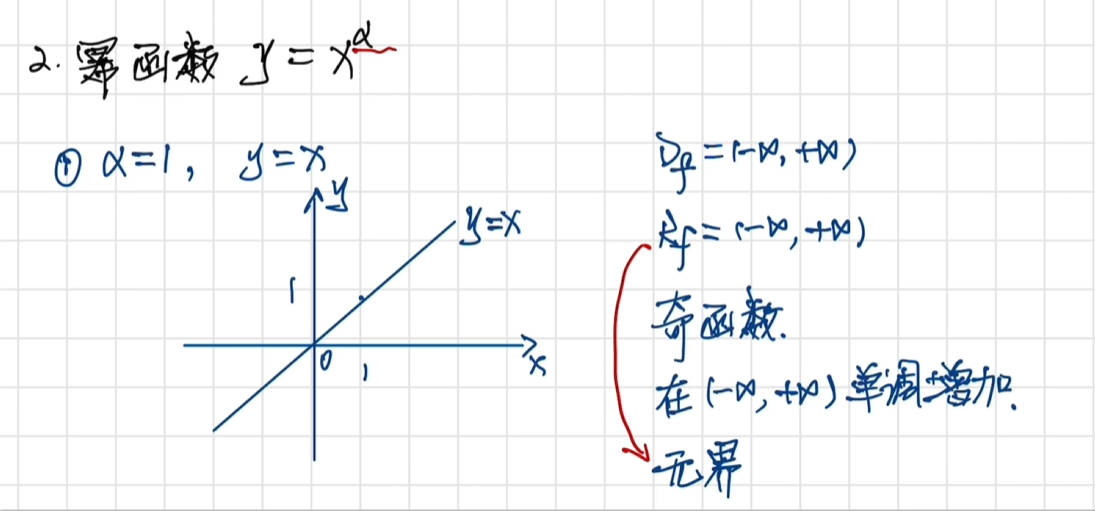
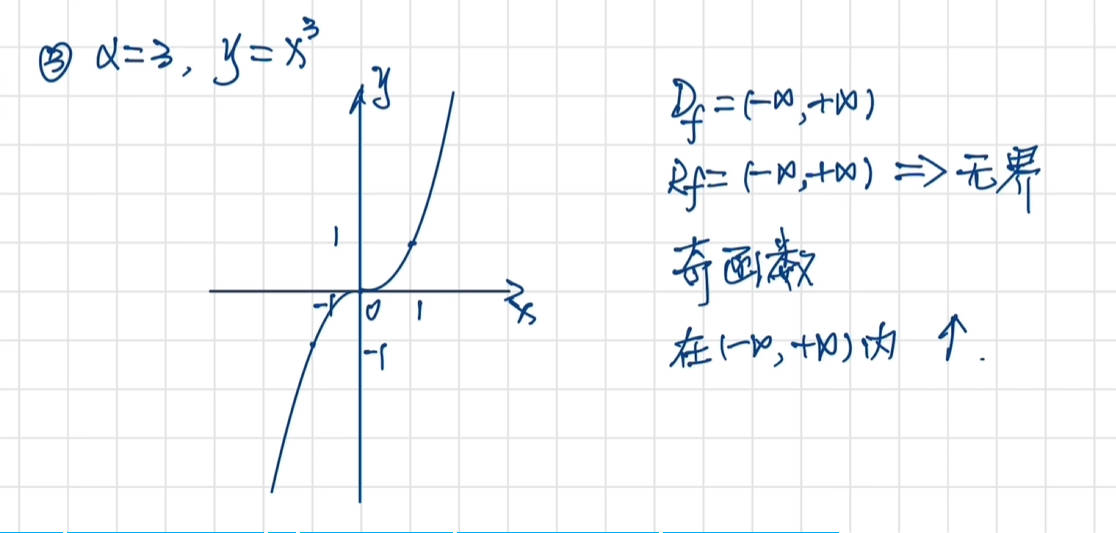
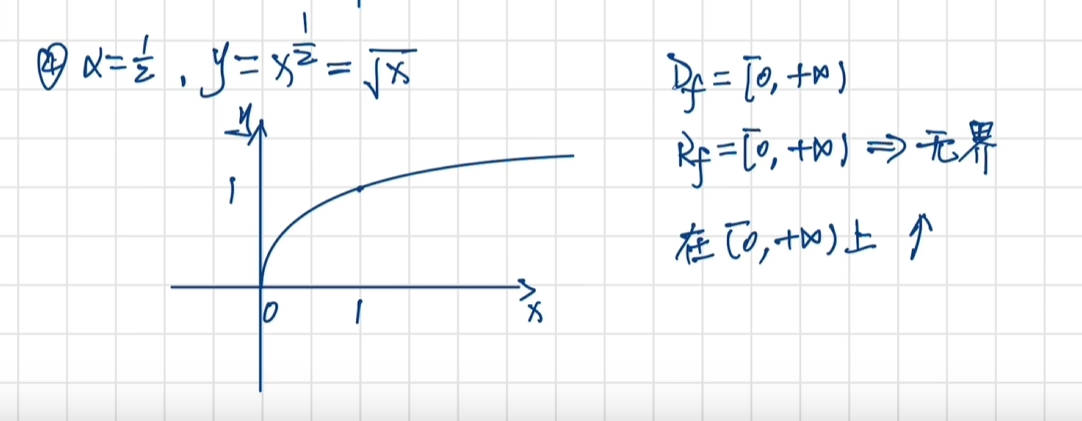
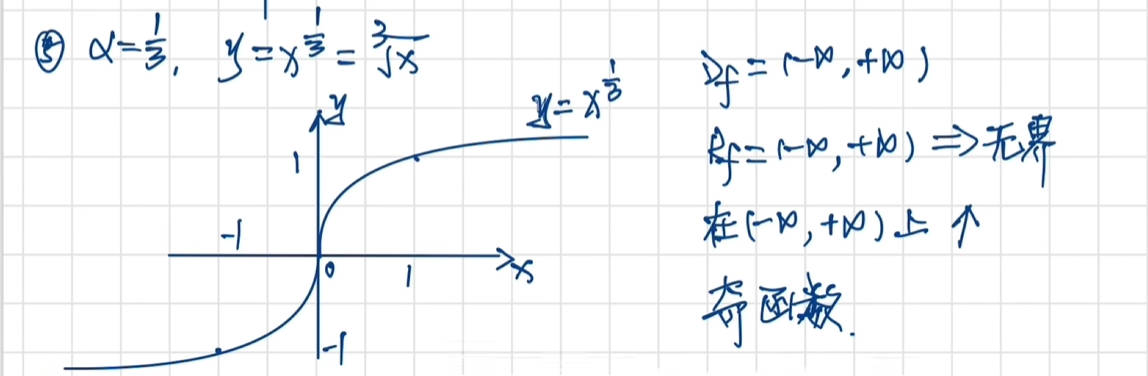
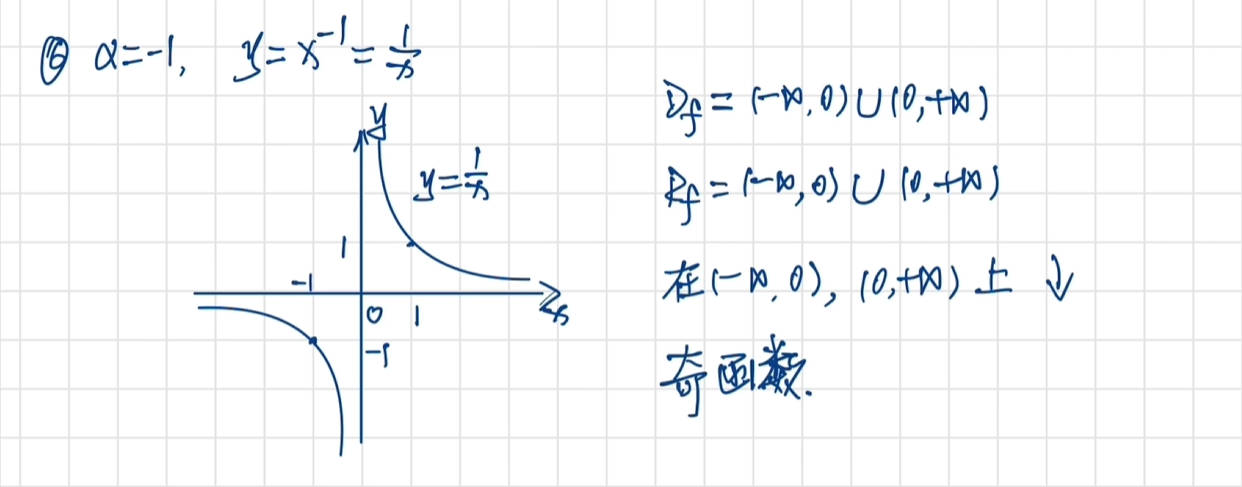
幂函数
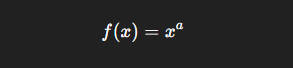
x是自变量
a是一个常数(可以是正数、负数、分数或整数)。
当 a 为正整数时,幂函数就是多项式中的单项式;当 a 取非整数值或负值时,其定义域和性质会有所不同。
定义域与奇偶性

图像

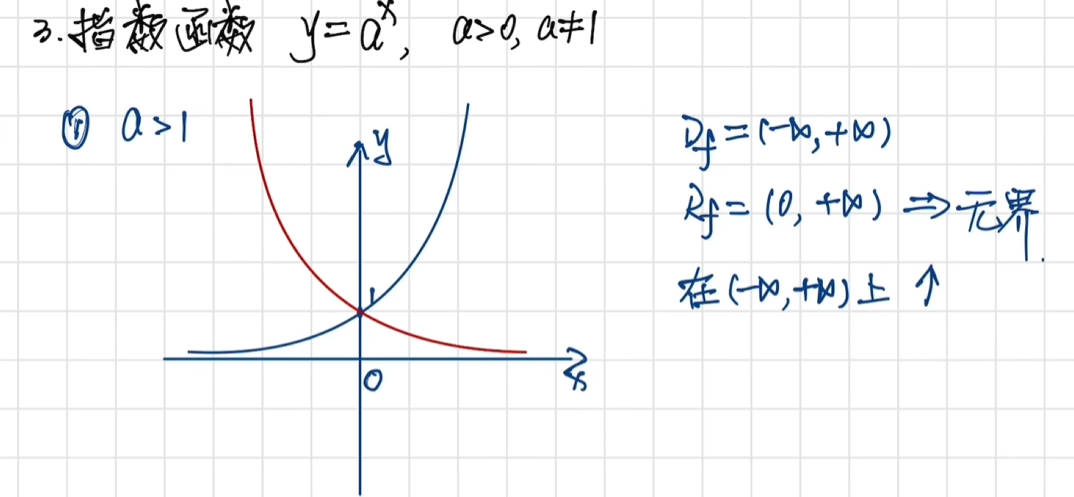
指数函数

底数 a 是常数,满足 a>0 且 a≠1;
指数部分是变量 x。
特别说明: 当底数 a=e(自然常数,约等于2.71828)时,函数 f(x)=e^x 被称为自然指数函数,具有许多优美的性质。

图像特点

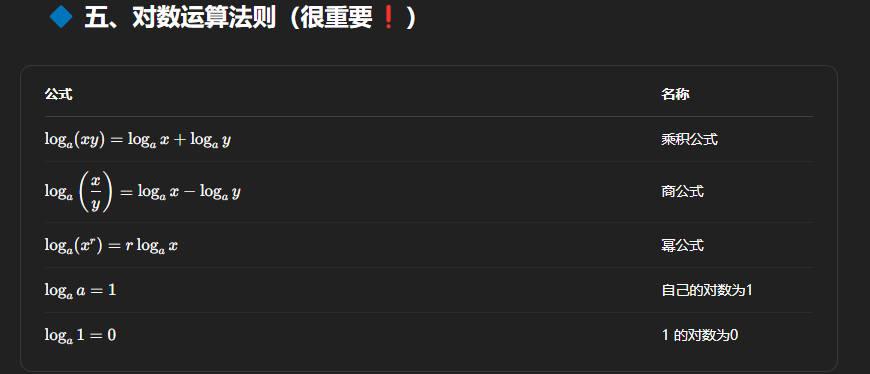
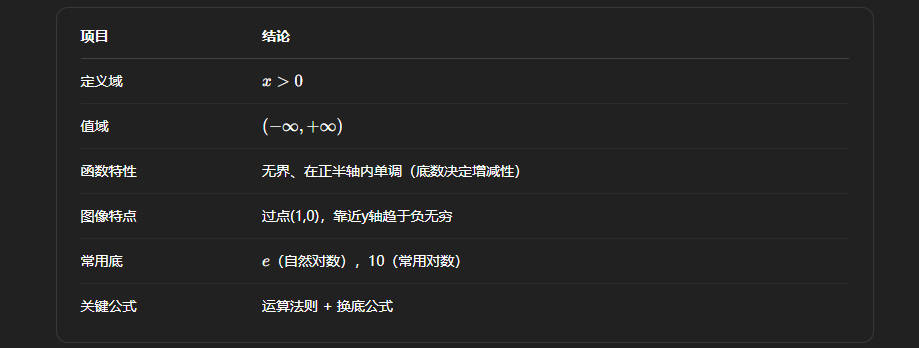
对数函数
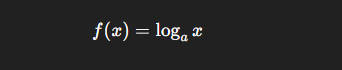
底数 a 必须满足:a>0 且 a≠1;
变量 x 必须满足:x>0。
对数函数表示“a 的什么幂等于 x”,即满足
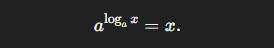
当底数取自然常数 e 时,函数写作
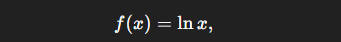
基本性质

图像特点

三角函数
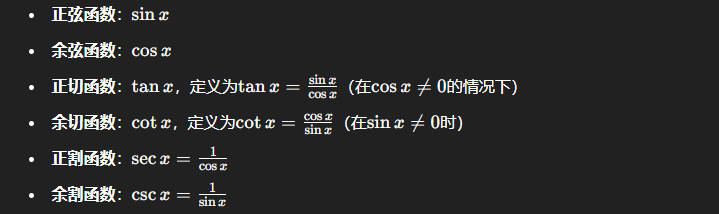
反三角函数

数列极限的定义

一个数列不收敛,就说它没有极限,或者说它是发散的
收敛数列的性质
唯一性
有界性
保号性
收敛数列与其子数列之间的关系
如果一个数列 {a_n}收敛于极限 A,那么它的任意一个子数列也收敛,且极限也为 A。
函数极限
定义

单侧极限
无穷极限
性质
唯一性
有界性
保号性
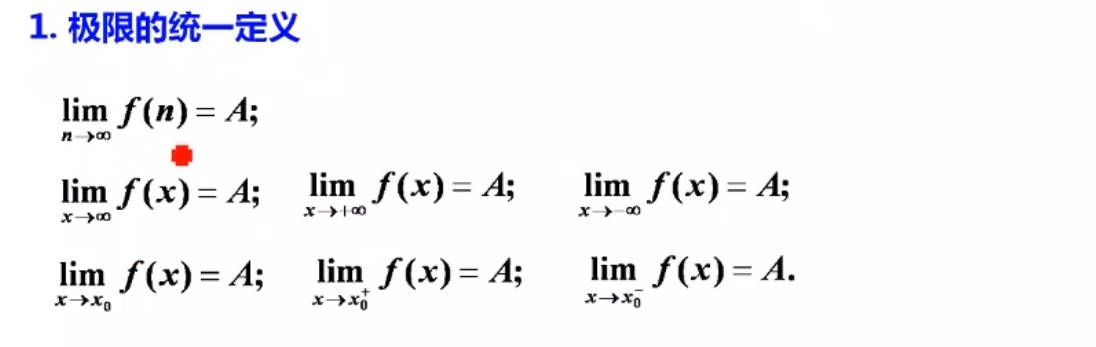
无穷
无穷小


无穷大


极限的运算法则
定理1:两个无穷小的和是无穷小
定理2:有界函数与无穷小的乘积是无穷小
推论1:常数与无穷小的乘积是无穷小
推论2:有限个无穷小的和也是无穷小

无穷小的运算法则
极限四则运算法则(计算商的时候分母不能为0)
复合函数极限运算法则(内层函数不能为0)
求函数极限的方法
分式函数求极限的求法
代入法
零比零型约去分母0因子
无穷比无穷型,分子分母同除以最高次幂
复合函数求极限
设中间变量
零比零型极限问题
利用平方差公式,立方差公式,因式分解来提取、消去零因子。
无穷比无穷型
找出分子、分母的最高次项
所有项都除以最高次项(一般是分母的最高次幂)
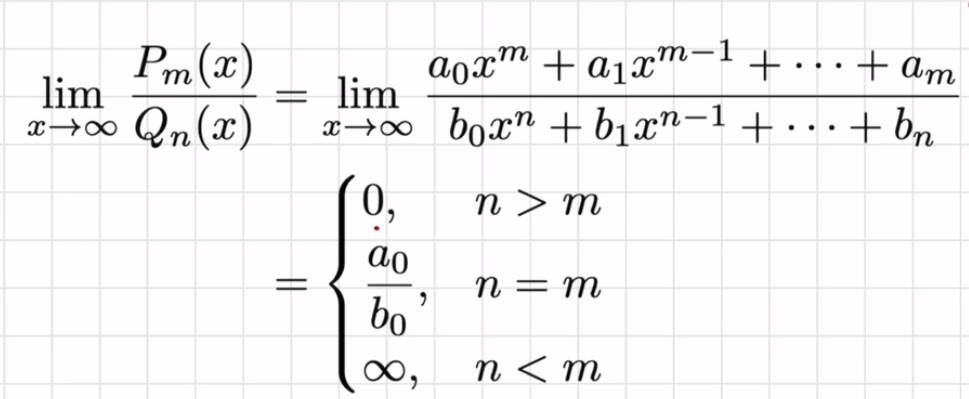
极限存在法则及两个重要极限
夹逼准则

单调有界函数必有极限


两个重要极限
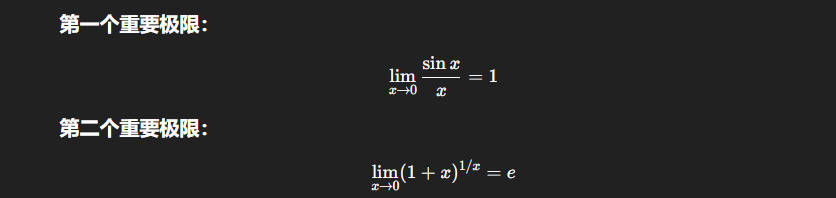




无穷小的比较
两个无穷小的和差积仍然是无穷小,但是对于商会有不同的情况。


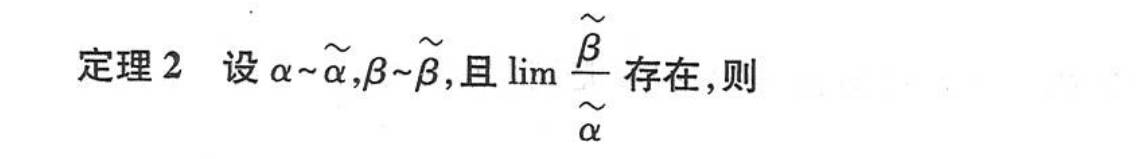
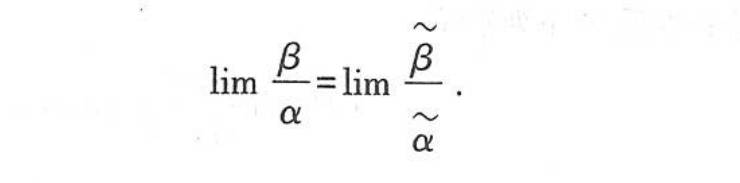

等价无穷小的代换
代换原则:乘除关系可以代换
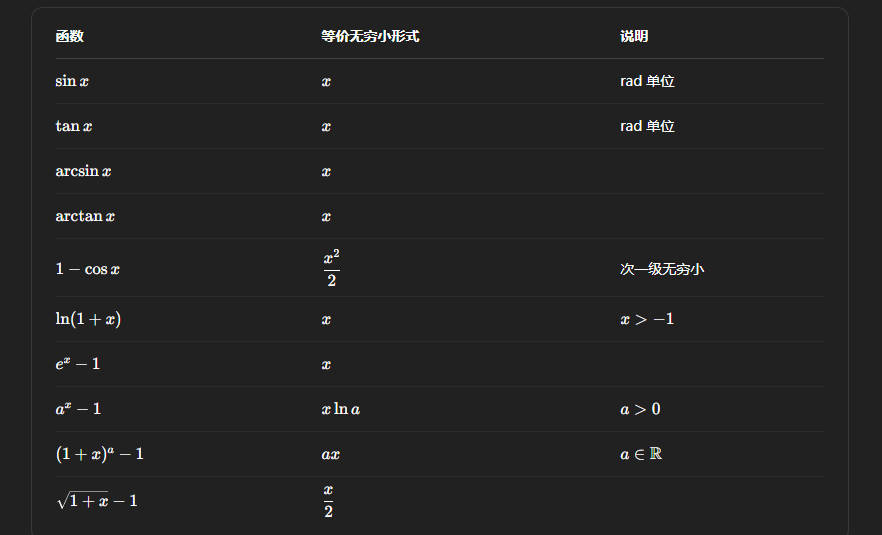
常见的等价无穷小



函数的连续性与间断点
连续性
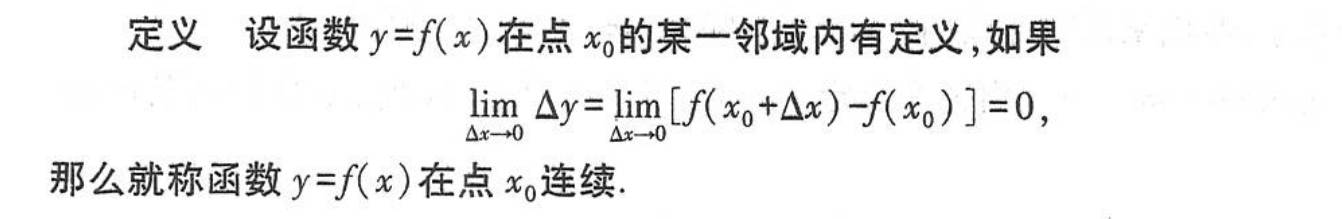
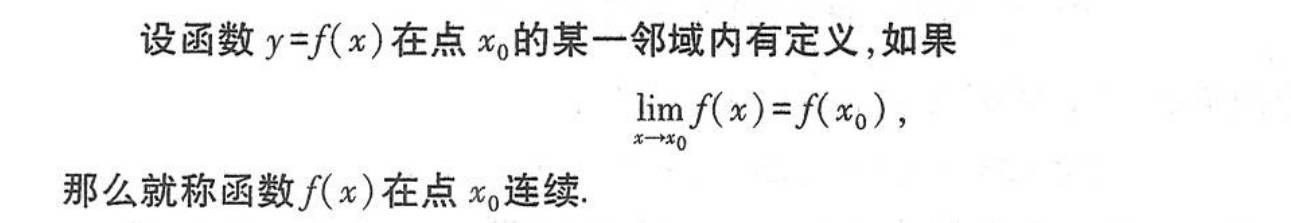

间断点


求极限的步骤

连续函数及其性质

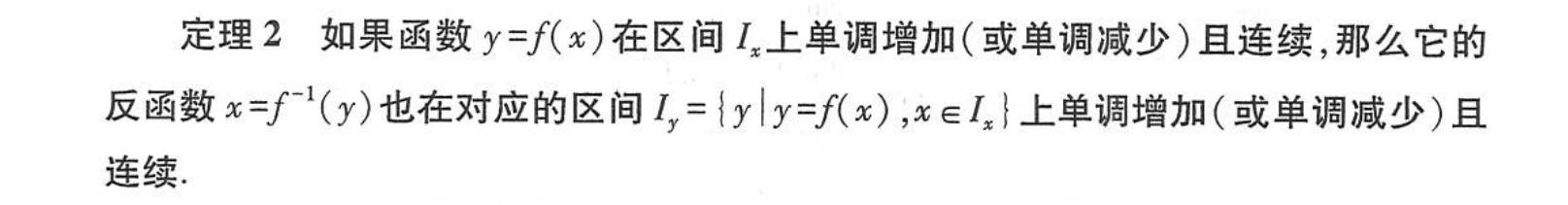
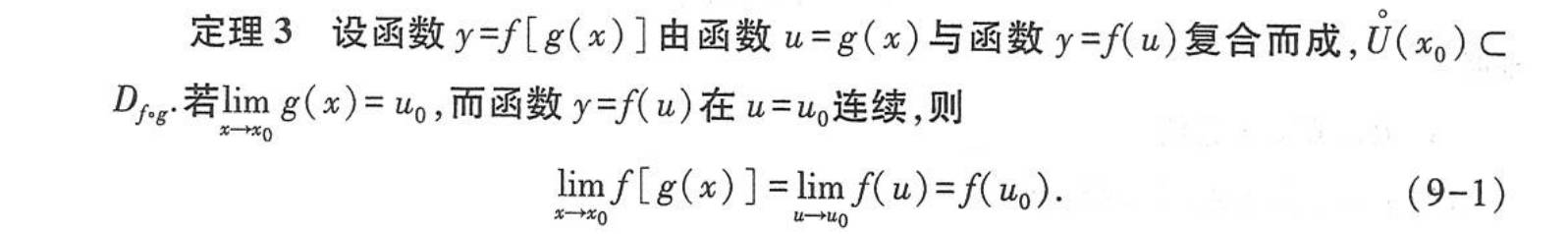
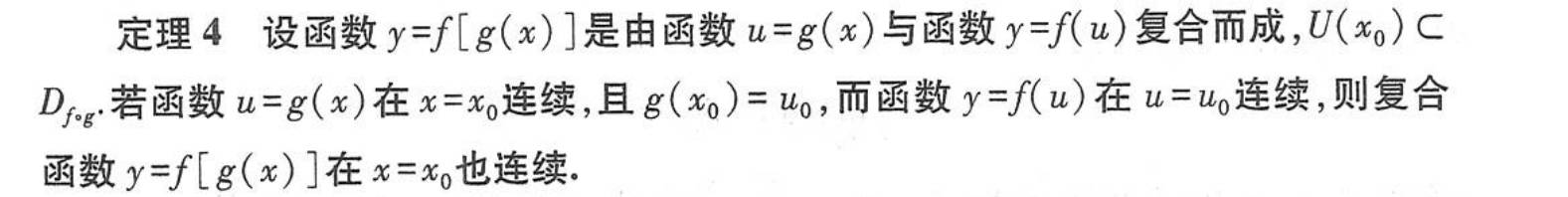

闭区间上连续函数的性质



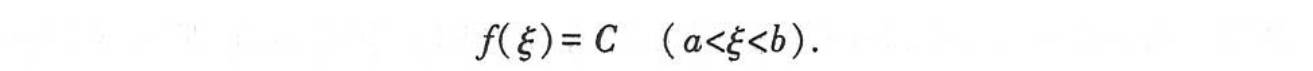

导数与微分

费马引理
证明过程

罗尔定理
证明过程

拉格朗日中值定理
推论
导数恒为零的函数必为常数函数

